【技术前沿】随机地图定位的思考

作者：技术部　杨盛海

　　几乎人人都用过地图，你如果去另外一个城市旅游，下车第一件事就是买张地图。如今网络的发展催生了新式的地图——电子地图，更加方便了人们的生活。无论你是使用电脑上网还是手机上网，都可以登录网上的电子地图，直接搜索最快捷到达目的地的方式，方便至极。电子地图相较于纸质地图，不仅可以浏览，而且可以随意缩放以及运算，如计算两地距离，统计办事处数量等。

　　任何地图都是基于一定的坐标系来绘制，世界地图可以有多种不同的坐标系，用户最熟悉的是最广泛的是经度－纬度坐标，也是用户最容易接受的坐标系。网上应用最多的Google地图也是采用了这种坐标方式，而且Google地图也提供了基于这种方式的API，方便用户进行二次开发。

　　对于最终用户来说，也许并不需要知道经纬度这一概念，但是如果要在地图上开发，放置各种覆盖物，如标记、文本等，则必须是要透彻理解的。下面就简单说一下经纬坐标概念。

　　地球围绕地轴自转，地轴与地球表面相交于两点，称为南极和北极，地球绕地轴转一圈，地表形成的周长最长的轨迹称为赤道。规定赤道的纬度为0度，北极的纬度为90度，南极的纬度为-90度。地球表面上的任何一点与赤道平面的交角，其度数称为该点的纬度，北半球为正的度数，南半球为负的度数。再来看经度，把地球看作一个 剥了皮的桔子，沿着平行于地轴的方向把地图等分为360份，也就是把这桔子分360个桔子瓣，每一个瓣是一个经度数，从英国某个天文台开始计数，为0度，向西为西经，向东为东经，一般规定西经为负的经度，最小为-180度，东经为正的经度，最大为180度，应该说正180度和负180度是重合的。这样一来，地球上任何一点都可以由一个经纬度坐标表示：(x,y),x大于等于负180，小于等于正180。y大于等于负90度，小于等于90度。所以定位地球上的某一点，只需要一个经纬度坐标就可以了。由于地球表面面积非常大，定位某一个目标，需要把经纬度精确到小数点后面好几位数才行，如故宫西南角的坐标为(116.392,39.913)。

　　经纬度的概念明确之后，现在考虑一个问题：在全世界范围内随机定位地图上的某一点。这是一个比较有意思的题目。想想我们随便产生一个合理的经纬度，它就能定位到地球上 某一个不知名的地点，这个地点有可能是南美的热带雨林，也有可能是有非洲的热带沙漠，当然更有可能是浩瀚的太平洋。最初想到这个问题，我只需要几秒钟就能想到，只要随机产生一个-180到180之间的经度数以及一个-90度到90度的纬度就可以了。大脑飞快运转起来，利用Google提供的免费的世界地图以及方便的Javascript脚本接口，我很快实现出来了。然而，结果却不能让人满意，地图经常定位到渺无人烟的俄罗斯西伯利亚北边的苔原以及万年冰封的南极大陆，而且概率很高。

　　静下心来简单地想了一下，原来我把立体的地图平面化了.为了简单起见，我们来看下面这张图，它是Google提供的世界全图，大家看出来有什么奇怪的地方吗？

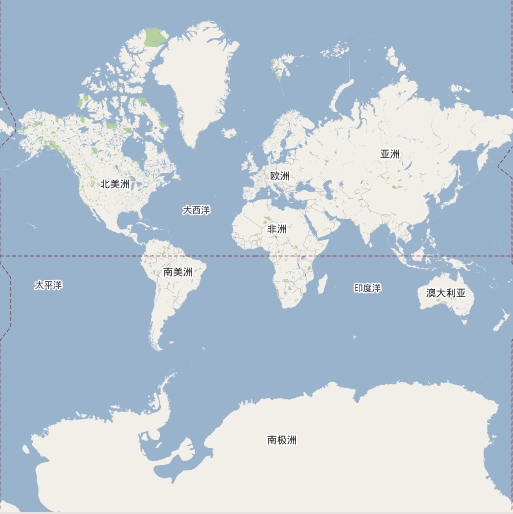
　　原来，这张地图就是简单地把球体表面拉伸为平面了，经过这样处理之后，两极及其附近的区域产生了很大程度的扩展，尤其是南极大陆，差不多占了整个陆地面积的一半，这显然是不合理的。

　　不过这并不是说Google做错了，事实上把球面平铺成平面本来就没有完美的解决办法。我们要产生任意的定位点，就是基于这张平面地图了，所以高纬度的地方命中的机率比较大。所以，因为平面地图不合理，我们的随机方法也是不合理的。

　　接下来，我们只能在球体表面产生随机地点，也就是越接近赤道的地方，命中概率越高，越接近两极的地方命中率越低。很容易想象，从-180到180之间随机产生一个经度，是很容易的，无论是接近两极，还是接近赤道，经度都是均匀分布的。整个问题最关键的地方就是，如何产生一个随机的纬度。Javascript产生的随机数是从0到1之间均匀分布的，我们需要找到纬度与0到1之间的对应关系。为了简单起见，我们把纬度为90定义为0点，把纬度为0定义为1点，那么某个纬度就可以对应于0和1之间的某个数，就看怎么对应比较合理。

　　我们做如下想象，把一根极细的足够长的带子从北极开始，绕着地轴一圈一圈地铺在北半球表面，一直铺到赤道，把整个带子的长度定为1，那么，某个纬度所在的位置必然为带子上的某一点，那么重新把带子抻开来，一头是北极，一头是赤道，带子上的这个点距离北极点的距离就是这个点的纬度所对应的那个从0到1之间的数，这个想法是比较合理的。这个数值可以用比值来确定，真正带子的长度是一个很大的数，把这个点转化为0到1的数可以用比值来获得，即从这点到北极的距离除以从北极到赤道的距离。把带子理想化之后，这个比值实际上就成了这个纬度点以北的球冠的表面积与整个北半球的表面积之比。问题到这里就豁然开朗了！

　　中学立体几何学过，球冠的表面积是与球冠的高成正比的，要比表面积，只需要比高就可以了，到这里问题又进一步简化了，假设半径为1，半径也就是整个北半球的高，纬度为x，球冠的高比上半径就是(1-sin(x))/1。这个值对应的随机数假如是随机函数产生的rand，那么这个式子就是：1-sin(x)=rand，这个纬度值就是arcsin(1-rand)。

　　北半球的纬度得出来，再乘一个随机的1或者-1就得出整个地图的纬度。用Javascript一试，呵呵，果然不再定位到南极洲。基本上比较完美，除了经常定位到太平洋里去。

　　随机定位地图这个问题不是很难的问题，不过对于数学没学好的同学还是需要动一番脑筋的，即使不难的问题，完美解决之后仍会有一种成就感，这就是勤于动脑所带给程序员的快乐。